Bildungsgesetz für magische Quadrate gerader Ordnung
Hier ist die Anleitung, wie man magische Quadrate beliebiger Größe mit gerader Seitenzahl erzeugt. Es wird unterschieden zwischen doppelt gerader Ordnung (Seitenlänge ist durch 4 teilbar) und einfach gerader Ordnung (Seitenlänge ist durch 2 teilbar aber nicht durch 4). Die magische Summe ist immer (n³ + n) · ½.
Bildungsgesetz für magische Quadrate 4×4
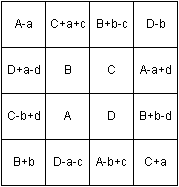
Jupiteramulett: A=11, B=7, C=6, D=10, a=7, b=9, c=1, d=8
Die magische Summe ist 34.

Magische Quadrate doppelt gerader Ordnung
n ist durch 4 teilbar.
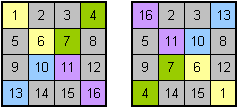
- Trage die Zahlen von 1 bis n² zeilenweise in ihrer natürlichen Reihenfolge in die Matrix ein
- Spiegle Elemente, die diagonal-symmetrisch zur Mitte des Quadrates sind. Also gelb mit violett und grün mit blau.
Selbiges am Beispiel eines magischen Quadrates 8×8
Hier erkennt man die Komplexizität des Algorithmus, da zusätzlich zu den Spiegelungen um den Quadratmittelpunkt noch Spiegelungen um jeden der 4 Quadrantmittelpunkte hinzukommen.
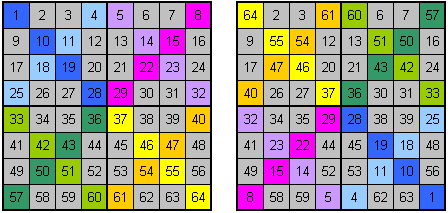
Die magische Summe dieses 8×8-Quadrates ist 260.
Magische Quadrate einfach gerader Ordnung
n ist durch 2, aber nicht durch 4 teilbar.
Teile das Quadrat in 4 Quadranten.
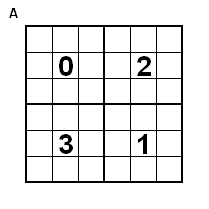
Jeder Quadrant wird mit dem Bildungsgesetz für magische Quadrate ungerader Ordnung befüllt.
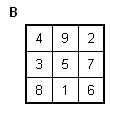
Es wird in der angegebenen Reihenfolge mit dem Quadrat der Ordnungszahl (in diesem Beispiel ist die Ordnungszahl 3, also 3² = 9) multipliziert.
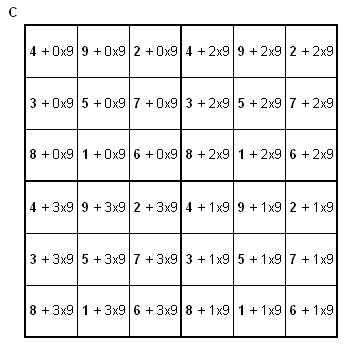
sodaß folgendes Quadrat entsteht:

Vertauschen:
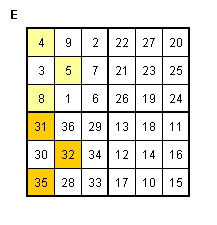
Fertig!
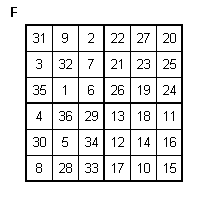
Die magische Summe des 6×6-Quadrates ist in diesem Beispiel 111.
Selbiges am Beispiel eines magischen Quadrates 10×10
Hier werden die Vertauschungen schon etwas komplexer.
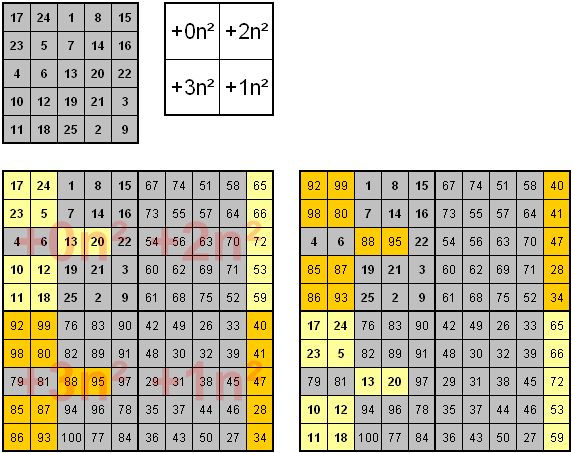
Alternativmöglichkeiten für die Vertauschung:
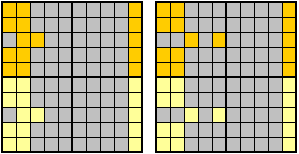
Die magische Summe eines magischen Quadrates mit Seitenlänge 10 ist 505.
